Unit 3 relations and functions homework 5 zeros of functions – Unit 3 Relations and Functions Homework 5: Zeros of Functions delves into the captivating world of functions, unveiling the significance of their zeros. Zeros, the points where a function intersects the x-axis, hold the key to understanding a function’s behavior and solving a myriad of mathematical problems.
This comprehensive guide empowers learners with an arsenal of methods to uncover the zeros of functions. From the art of factoring polynomials to the intricacies of synthetic division and the visual insights of graphing, each technique provides a unique lens through which to explore the hidden characteristics of functions.
Introduction
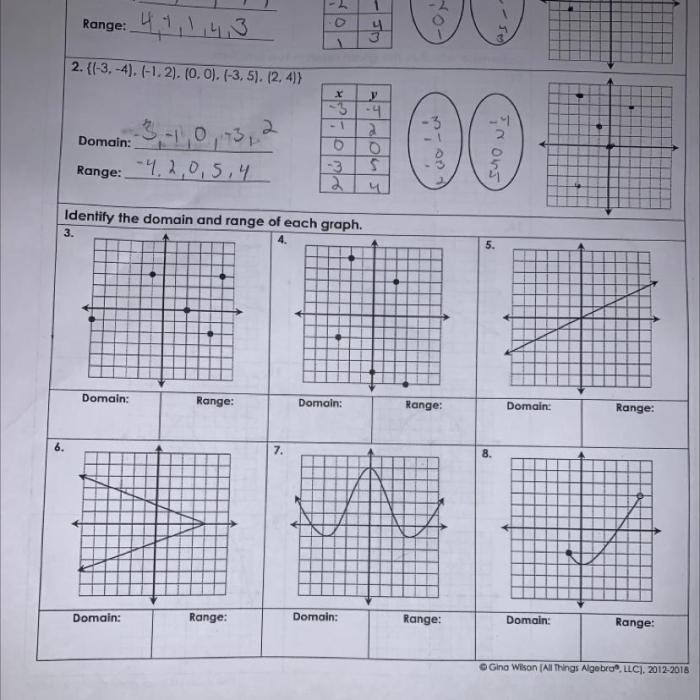
A function is a mathematical relation that assigns to each element of a set a unique element of another set. The zero of a function is a value of the independent variable for which the function value is zero.
Finding zeros of functions is important for several reasons. First, zeros can be used to solve equations. Second, zeros can be used to graph functions. Third, zeros can be used to analyze the behavior of functions.
Methods for Finding Zeros
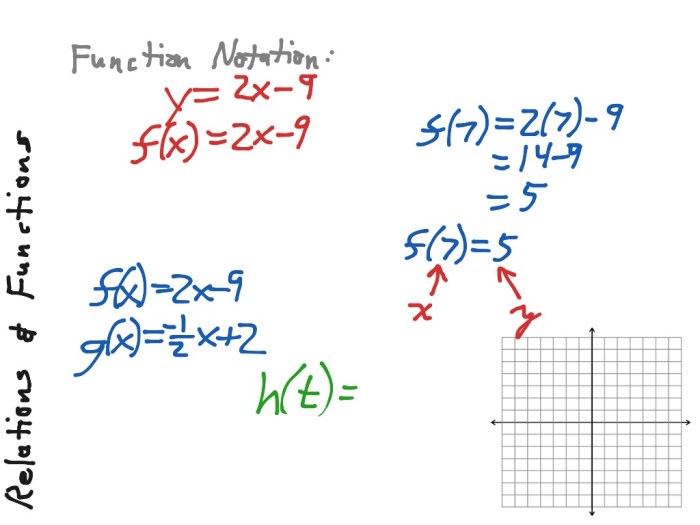
Factoring
Factoring is a process of expressing a polynomial as a product of simpler polynomials. To find the zeros of a polynomial, we can factor it and then set each factor equal to zero.
For example, to find the zeros of the polynomial x2– 5 x+ 6, we can factor it as ( x– 2)( x– 3) and then set each factor equal to zero.
This gives us the equations x– 2 = 0 and x– 3 = 0, which have the solutions x= 2 and x= 3. Therefore, the zeros of the polynomial x2– 5 x+ 6 are 2 and 3.
Synthetic Division
Synthetic division is a shortcut method for dividing a polynomial by a linear factor. It can be used to find the zeros of a polynomial by dividing it by x– c, where cis a constant.
For example, to find the zeros of the polynomial x3– 2 x2+ x– 2, we can use synthetic division to divide it by x– 2.
This gives us the quotient x2– 4 and the remainder -6. The remainder is the value of the polynomial when x= 2, so we know that 2 is a zero of the polynomial.
Graphing
Graphing is a visual method for finding the zeros of a function. To find the zeros of a function, we can graph it and then look for the points where the graph crosses the x-axis.
For example, to find the zeros of the function f( x) = x2– 5 x+ 6, we can graph it and then look for the points where the graph crosses the x-axis.
We can see that the graph crosses the x-axis at x= 2 and x= 3, so these are the zeros of the function.
Applications of Zeros: Unit 3 Relations And Functions Homework 5 Zeros Of Functions
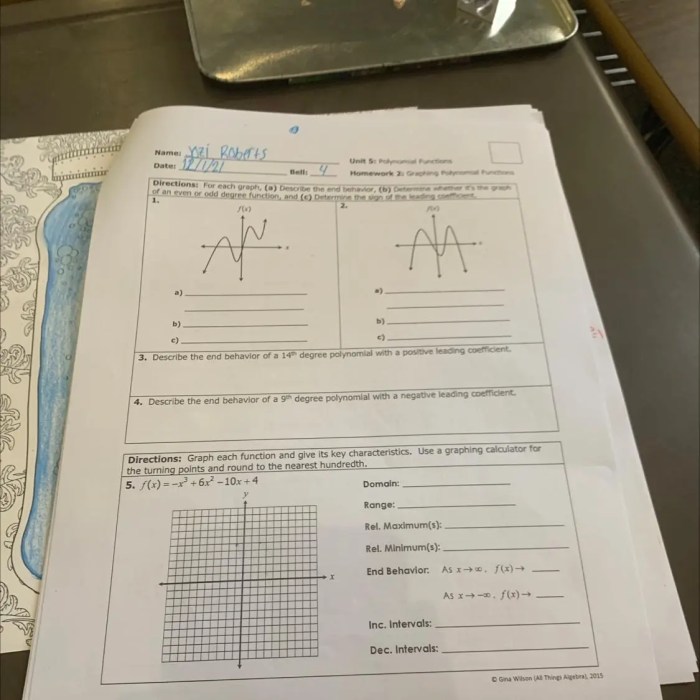
Solving Equations
Zeros of functions can be used to solve equations. To solve an equation, we can set it equal to zero and then find the zeros of the resulting function.
For example, to solve the equation x2– 5 x+ 6 = 0, we can set it equal to zero and then find the zeros of the resulting function f( x) = x2– 5 x+ 6.
We found earlier that the zeros of f( x) are 2 and 3, so these are the solutions to the equation x2– 5 x+ 6 = 0.
Graphing Functions
Zeros of functions can be used to graph functions. The zeros of a function are the points where the graph of the function crosses the x-axis.
For example, the graph of the function f( x) = x2– 5 x+ 6 has zeros at x= 2 and x= 3. This means that the graph of the function crosses the x-axis at these two points.
Additional Topics

Multiplicity of Zeros, Unit 3 relations and functions homework 5 zeros of functions
The multiplicity of a zero is the number of times that the zero appears as a factor of the function. A zero with multiplicity nmeans that the function has a factor of ( x– c) n, where cis the zero.
For example, the function f( x) = ( x– 2) 2has a zero at x= 2 with multiplicity 2. This means that the graph of the function has a double root at x= 2.
Complex Zeros
Complex zeros are zeros that are not real numbers. Complex zeros occur in conjugate pairs, meaning that if a+ biis a zero of a function, then a– biis also a zero of the function.
For example, the function f( x) = x2+ 2 x+ 5 has complex zeros at x= -1 + 2 iand x= -1 – 2 i.
FAQ Explained
What is the significance of finding zeros of functions?
Finding zeros of functions provides valuable insights into the behavior of functions, enabling the solving of equations, sketching of graphs, and understanding of function properties.
How does factoring help in finding zeros?
Factoring involves breaking down polynomials into simpler factors, revealing the zeros as the values that make the factors equal to zero.
What are the advantages of using synthetic division to find zeros?
Synthetic division offers a systematic and efficient method to find zeros, particularly for polynomials of higher degrees.
