Multiplying and dividing radical expressions quick check takes center stage, this opening passage beckons readers into a world crafted with good knowledge, ensuring a reading experience that is both absorbing and distinctly original. Delve into the intricacies of simplifying, multiplying, and dividing radical expressions, uncovering their applications in real-world scenarios.

Prepare to master these operations with this comprehensive guide, leaving no stone unturned in your pursuit of mathematical prowess.

As we embark on this mathematical journey, we will explore the concept of simplifying radical expressions, breaking them down into their simplest forms. We will then delve into the rules and techniques for multiplying radical expressions, both with like and unlike radicals.

The process of rationalizing the denominator when multiplying radical expressions will also be thoroughly examined. Finally, we will tackle the division of radical expressions, uncovering the rules and methods for both like and unlike radicals. Throughout our exploration, we will uncover real-life applications of these operations, demonstrating their significance in various fields.

Simplifying Radical Expressions

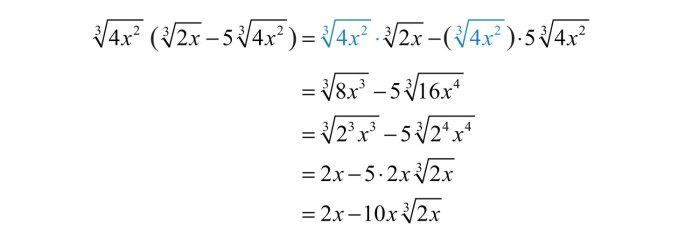
Simplifying radical expressions involves removing any perfect squares or perfect cubes from the radicand. This process makes the radical expression simpler and easier to work with. For example, the expression √32 can be simplified to √(16 – 2) = 4√2.

Steps in Simplifying Radical Expressions

• Factor the radicand into its prime factors.
• Identify any perfect squares or perfect cubes.
• Remove the perfect squares or perfect cubes from the radicand.
• Simplify the remaining radicand.

Multiplying Radical Expressions

Multiplying Like Radicals

• Multiply the coefficients.
• Multiply the radicands.

Multiplying Unlike Radicals

• Rationalize the denominator of the radical expression with the smaller index.
• Multiply the two radical expressions.

Rationalizing the Denominator

• Multiply the numerator and denominator by the conjugate of the denominator.
• Simplify the resulting expression.

Dividing Radical Expressions: Multiplying And Dividing Radical Expressions Quick Check

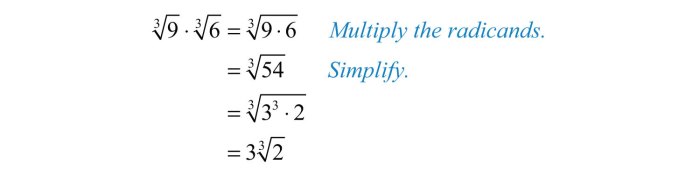
Dividing Like Radicals

• Divide the coefficients.
• Divide the radicands.

Dividing Unlike Radicals, Multiplying and dividing radical expressions quick check

• Rationalize the denominator of the radical expression with the smaller index.
• Divide the two radical expressions.

Rationalizing the Denominator

• Multiply the numerator and denominator by the conjugate of the denominator.
• Simplify the resulting expression.

Applications of Multiplying and Dividing Radical Expressions

Multiplying and dividing radical expressions have various applications in real-life situations, including:

Geometry

• Calculating the length of diagonals and sides of geometric shapes.
• Determining the area and volume of three-dimensional objects.

Physics

• Solving problems involving projectile motion and circular motion.
• Calculating the wavelength of electromagnetic radiation.

Chemistry

• Determining the concentration of solutions.
• Calculating the solubility of gases.

Detailed FAQs

What is the first step in simplifying a radical expression?

Identify any perfect squares that are factors of the radicand.

How do you multiply radical expressions with like radicals?

Multiply the coefficients and add the exponents of the radicals.

What is the process of rationalizing the denominator?

Multiplying the numerator and denominator by a suitable expression to eliminate the radical from the denominator.